二種二次試験電力管理過去問、H17問5,6、補足。

ここの補足、です。
問題文、解答内容については、ここ参照で。


問５
【解説】
送 電線と通信線が接近しているとき、相互の誘導的結合によって、通信線に電圧が誘起される現象を電磁誘導といい、通常、高電圧の三相送電線は故障以外はほと んどバランスして相電流が流れているので、大電流が流れてもある程度通信線が離れていると、各相と通信線の間の相互インダクタンスはほとんど等しく、電磁 誘導電圧は生じない。

しかし、送電線に地絡が発生して過大な電流が流れると、その大地を帰路とする電流成分による電磁
導作用によって、通信線に大きな電磁誘導電圧を生じ、通信線の作業員に危害を加えたり、通信機器を破壊するなどの障害を与えるおそれがある。

（１）異常時誘導電圧（１線地絡故障）の求め方
送電線に１線地絡故障が発生したときに、電磁誘導により通信線に発生する誘導電圧Ｖｍ（Ｖ）を表す式は、次のように求めることができる。

電磁誘導障害は第１図（添付）のように原理的には相互インダクタンスを持つ電気回路で考えられ、閉
回路の相互交さ磁束によって生ずる。

したがって、図のようにＩｅ、φ、ｅの正方向を決めれば、通信線に生じる単位長あたりの誘導電圧は、

ｅ＝ｄφ／ｄｔ

ここで両導体間の相互インダクタンスをＭ（Ｈ／ｍ）とすると、Ｍｉ＝Ｎφ→φ＝Ｍｉ／Ｎを代入し、

ｅ＝Ｍ （ｄ／ｄｔ） ・Ｉｅ ｓｉｎωｔ
　＝ωＭＩｅ ｃｏｓ ωｔ　（Ｖ）

次にＤ（ｍ）を乗じ絶対値を求める。

∴Ｖｍ＝|ｊωＭＩｅＤ|＝２πｆＭＩｅＤ（Ｖ）

が求まる。また、三相送電線を考えると、各相の電線と通信線間の相互インダクタンスの相違を無視して、第２図（添付）のように、Ｍａ≒Ｍｂ≒Ｍｃ≒Ｍとすると、

Ｖｍ＝ｊ２πｆＭＤ（Ｉａ＋Ｉｂ＋Ｉｃ）
　＝ｊ２πｆＭＤ３Ｉ０（Ｖ）

で表される。ただし、上式のＩ０は零相電流を表す。
したがって、上式より電磁誘導は送電線の零相電流によって誘起される事がわかる。

（２）電磁誘導障害対策
電磁誘導電圧の制限値はわが国では、中性点直接接地方式の超高圧送電線の場合は４３０（Ｖ）、０．１秒その他の送電線では、３００（Ｖ）を基準としていることは前述（メイン）の通りである。

国際電信電話諮問委員会では、一般の送電線では４３０（Ｖ）、０.２秒（小電流の場合、最大０.５秒）以内に故障電流が除去できる高安定送電線では、人体の危険が大幅に減少するので、６５０（Ｖ）までを許容している。

（ａ）送電線側の対策
解答（メイン）参照

（ｂ）通信線側の対策
１．ルートを変更して送電線の隔離を大きくしたり、交さする場合はできるだけ直角とする。
２．アルミ被誘導遮へいケーブルのような特殊遮へいケーブルを採用し、遮へい係数を６０（％）以下にする。
３．通信回線の途中に中継コイルあるいは高圧用誘導遮へいコイルを挿入して、誘導こう長を短くすることにより、誘導電圧を分割または軽減する。
４．避雷器や保安器を設置する（Ｖ－ｔ特性のよいもの、避雷器の接地はＡ種）。
５．通信線と送電線の間に導電率のよい遮へい線を設ける（通信線に近く設置するほど効果は高い）

問６
【解説】
この問題は、ある系統負荷に複数台の火力発電機で電力を供給する場合、どのように負荷を配分すると最も経済的であるかを求めるものである。一般的にこの種の問題については等増分燃料費法（等増分率配分法ともいう）がとられている。

ここで説明を簡単にするために、第１図（添付）のような発電機２機系統について考えてみる。この場合の供給力と系統負荷の間には次の関係がある。

Ｐ１＋Ｐ２＝ＰＲ　　（１）

また、それぞれの発電機の燃料費をＦ１、Ｆ２として、総燃料費をＦとすると、

Ｆ１＋Ｆ２＝Ｆ

となる。さらに燃料費は発電機出力の関数として表せるから、

Ｆ１＋Ｆ２＝ｆ（Ｐ１）＋ｆ（Ｐ２）＝Ｆ　　（２）

となる。すなわち火力系統の経済運用とは（１）式で示される需要条件のもとで、総燃料費Ｆを最小とするＰ１およびＰ２を求めることである。

これについては、「ラグランジュの未定係数法」が用いられる。それにはラグランジュの未定係数をλとして目的関数をφとすると、

φ＝Ｆ－λＰＲ＝Ｆ１＋Ｆ２－λ（Ｐ１＋Ｐ２）

とおいて、

ｄφ／ｄＰ１＝０、ｄφ／ｄＰ２＝０

となる関係を求めれば良い。上式より、

ｄＦ１／ｄＰ１＝ｄＦ２／ｄＰ２＝λ

の関係が成立する。

この場合のλは、いわば火力発電機の増分燃料費であって、各機の増分燃料費が等しいときに、全燃料費が最小（最も経済的）になる事を示している。

以上、火力発電機２台について述べたが、多数（ｎ台）についても同様に考える事ができる。すなわち、

n
ΣＰｉ＝ＰＲ
i=1

また、等増分燃料費法より、
ｄＦ１／ｄＰ１＝ｄＦ２／ｄＰ２＝…
…＝ｄＦn／ｄＰn＝λ

として、多機系（ｎ台）の火力発電機の経済運用にも適用される。

この解法は、次の条件が満足された場合にのみ成立する。

１．対象とする火力発電機は平行運転されていること。
２．入力－出力曲線が連続的に増加していること（第２図のＦ曲線のように漸増していること）
３．増分燃料費が出力増大に伴って減少しないこと（第２図のｄＦ／ｄＰが漸増していること）

実際の電力系統の経済運用については、調整式水力発電所の水の有効利用、送電線の損失を最小（ロス・ミニマム）の条件などを総合勘案して運用がなされている。

ここにおいては、火力系統にのみについての問題を取り上げたが、水火力併用の経済運用についても第２種受験者はその概要程度の学習をしておくことが大切である。

二種二次試験電力管理過去問、H17問3,4、補足。

ここの補足、です。
問題文、解答内容については、ここ参照で。


問３
【解説】
（１）電線の抵抗と安全電流
電線に電流を通じたとき、抵抗による発熱によって電線の温度は上昇し、これがある温度以上になると材質に変化を生じ、電線の諸性能を低下させる。電線材質の変化は、過熱される時間と温度によって影響される。第２図にそれらの関係を示す（添付）。

図 からもわかるとおり長時間連続加熱しても機械的性能が低下しない温度として９０℃が標準の最高許容温度に推奨されている。このとき流しうる電流を、安全電 流又は連続許容電流という。また短時間なら温度を１００℃に上げても性能はほとんど変化しない。このとき流しうる電流を、短時間許容電流という。

つまり、抵抗によるジュール熱の発生が低減されれば損失が少なくなり、裏を返せば同じ損失まで許容されるならば、送電容量の増加を図ることができることになる。

一般に、送電容量を増加させるための方策としては、
・インダクタンスを減少する
・静電容量を増大する
・送電電圧を高める
などが挙げられる。

（２）コロナ放電による障害
送 電線にコロナが発生すると、電力損失、ラジオ障害、電力線搬送通信設備への障害、コロナ振動障害、消弧リアクトルの消弧力低下、直接接地系での誘導障害な ど種々の障害を引き起こす。ただし、雷サージが電線を伝搬してゆくときはコロナがその波高値を減衰させる役割を果たすという利点がある。

（３）コロナ放電発生の要因
架 空送電線では絶縁を施さない裸電線を使用し、その絶縁は空気に頼っている。このため送電電圧が高くなると、空気の絶縁性を考慮しなければならなくなる。空 気の絶縁耐力には限界があり、気温２０℃、気圧１０１３．２５ｈＰａの標準状態において、波高値で約３０ｋＶ／ｃｍ、実効値で２１．１ｋＶ／ｃｍの電位の 傾きに達すると空気は絶縁力を失い、電線表面から放電がはじまる。これをコロナ放電と呼び、次の性質がある。

１．薄光および音を伴い、電線、がいし、各種の金具などに発生する。
２．細い電線、素線数の多いより線ほど発生しやすい。
３．晴天の時よりも雨、雪、霧などのときのほうが発生しやすい。

架空送電線では細い素線を何本もより合せた「より線」を使用しているので、電線表面には凹凸があり、電線表面の電位の傾きは平等ではない。このため３０ｋＶ／ｃｍの電位の傾きを生じた部分にだけ、局部的に放電が生じる事になる。

電線表面全体が３０ｋＶ／ｃｍの電位の傾きとなればフラッシュオーバに至るが、コロナ放電はフラッシュオーバに達しない状態での持続的な部分放電であり、薄光および音を伴い、一般に電線、がいし、各種の金具などに発生する。

電線表面の電位の傾きがある値を超すと、空気が電離してコロナが発生するが、このコロナが発生し始めるような電位の傾き（コロナ臨界電位の傾き）は次の実験式によって求められる。

Ｅg0＝（３０／√２） δ^(2/3) （１＋0.301/rδ） （kV/cm）

ここで、δは相対空気密度であり、気圧ｐ（ｈＰａ）と気温ｔ（℃）により次式から求められる。

δ＝（０．２８９２ｐ）／（２７３＋ｔ）

δの値は、１０１３．２５ｈＰａ、２０℃のとき１となる。ｒは電線半径（ｃｍ）である。

実際の送電線では、電線の表面状態、天候などの影響を考慮に入れた字式（単導体方式の場合）が使用されている。

Ｅ0＝ｍ0ｍ1×４８．８δ^(2/3)｛１＋0.301/√（rδ）｝log10（D/r)　（ｋＶ）

ただし、
ｍ0：電線表面の状態に関係した係数であり、表面の精粗、素線数によって表１（添付）の値をとる（表面係数と呼ばれる）
ｍ1天候に関係する係数であり、雨天の時の空気の絶縁力の低下度を表し、晴天の時１．０、雨、雪、霧などの雨天の時０．８とする（天候係数と呼ばれる）。

問４
【解説】
％インピーダンス法で演算する。
基準容量を５０（ｋＶＡ）として、変圧器の％インピーダンスを基準容量換算する。３０ｋＶＡの％インピーダンス％Ｚ１は、

％Ｚ１＝５０／３０　×５＝８．３３　（％）

５０ｋＶＡの％インピーダンス％Ｚ２は％Ｚ２＝５（％）である。

次に基準電流ＩＢＡＳＥ（Ａ）を求めると、

ＩＢＡＳＥ＝ＳＢＡＳＥ／ＶＢＡＳＥ
　　＝５０×１０^3／２００＝２５０（Ａ）

したがって、短絡電流ＩＳ（Ａ）は、

ＩＳ＝１００／（％Ｚ１＋％Ｚ２） ×２５０
　＝１００／（８．３３＋５） ×２５０＝１８７５（Ａ）

となり、オーム法で求めた値と％インピーダンス法で求めた値は一致する。

この問題は、問１と同様、過去電験第３種に出題された問題の類題であり、電験第３しゅ受験時学習した基本的な事項を確実に覚えていれば、解答を簡単に導くことができる。

二種二次試験電力管理過去問、H17問12、補足。

ここの補足、です。
問題文、解答内容については、ここ参照で。

２００５年分へ突入。

問１
【解説】
この問題は過去電験３種に出題された問題の類題であり、電験第３種受験時に学習した基礎的な事項をしっかりと覚えていれば簡単に解くことができる問題である。平均流量、最大出力の公式は覚えておかなければならない公式である。

なお、電験第２種受験者は降雨量に関する次の諸公式も覚えておく必要がある。
１．流出高＝総流出量（ｍ^3）／流域面積（ｋｍ^2）×１００^-3 （ｍｍ）
２．損失高（ｍｍ）＝降雨量（ｍｍ）－流出高（ｍｍ）
３．損失率＝損失高（ｍｍ）／降雨量（ｍｍ）
４．流出係数＝流量（ｍ^3）／降水量（ｍ^3）

流出高は流出量（体積）を流域面積（面積）で除すれば高さとなる。
ここでいう高さは、単位面積あたりの高さ、である。
つまり、降雨量も単位面積あたりの高さ、とも表現できるため、降雨量に対する流出高（降った量に対して実際に水位が上がった量）の、差が損失高、割合が損失率ということになる。

また、高さ同様の係数として、流出係数は高さではなく、量（体積）の比率で表したもので、降水量に対する流量の比率となる。

問２
【解説】
（１）大容量変圧器の分解輸送と組立輸送
従来、大容量変圧器は、分解輸送が常識とされていたが、近年、大容量器の組立輸送の技術が発達し、山間の水力発電所のような特殊な場合を除いて、ほとんど組立輸送が可能になっている。

変圧器の組立輸送を行えば、現地組立室及びクレーンの省略、分解組立に要する工期と費用の節減など利点が多い。

このため、特に、
１．変圧器本体の重量と外形寸法の縮小
２．大容量変圧器輸送専用貨車の使用
３．輸送の為の特殊設計

な どについて種々工夫されていて、外鉄形変圧器においては、単相に分割した中身とタンクとを組立輸送し、現地で共通ベース上に組み立て、上部に共通ｶﾊﾞｰ をつけるもの（特別三相式構造）、内鉄形変圧器においては、輸送時の高さを切り詰めるための５脚鉄心の採用、鉄心の継鉄部分を取外して仮ふたを使用して輸 送するもの（分割三相式）などがあり、さらに、仮タンクで送られた三相変圧器２台を現地で同一のタンクに並べ入れ、１台の変圧器にする方法などがある。

（２）機器据付工事
機 器の据付は、架線工事などの上部作業が終了した後に行うのが好ましい。変圧器や遮断器などの現場組み立ての機器は防じん面で特に配慮する必要があり、気象 情報に留意し、組立現場周辺の車両の通行や土木工事などを中止して万全を図る。また変圧器など内部に人が入って作業する場合は、防湿、防じん、酸欠防止の ための乾燥空気の送り込み、着衣からのじんあい・工具の脱落防止のための専用作業服の着用などの配慮が必要である。

（３）大容量変圧器の真空乾燥と絶縁油の注入
真 空乾燥法は、大容量変圧器に最も適した方法で、所要日数も短く、乾燥も完全に行われる。第１図（添付）に示すように、外圧に耐えられるように補強した外箱 内に変圧器本体を入れ、内部に加熱管を入れてボイラから蒸気を送り、一方、内部を真空ポンプで３５（ｋＰａ）程度の真空として、水分の蒸発を促進させる。

外 箱内温度は８０～９０℃とし、復水器に凝結する水分の量を測定して、絶縁抵抗の変化とあわせ考慮して乾燥の進行程度を判定する。乾燥が終了すれば、真空を 破って中身をつり出し、各部の締付を点検調整の上、再び外箱内につり込み、常圧のままで１２時間以上再乾燥して、絶縁油脱気装置によって脱気脱水した油を 注入する。

（４）
ガス絶縁変圧器の水分・ういんあい・純度の管理
（ａ）水分の管理
ＳＦ６ガス中の水分は、外気温の変化により絶縁物表面に結露して絶縁低下の原因となったり、分解ガスと反応して活性なフッ化水素を生成し、絶縁材料を劣化させる原因となるため、ガス中の水分量は厳しく管理する必要がある。

通 常、分解ガスあるいはガス中の水分は合成ゼオライトなどの吸着剤によって管理値以下に吸着される仕組みになっているが、機器の据付時に吸着剤が大気中に長 時間さらされるので、所要の新しい吸着剤と交換し、３０分以内に真空引きを開始することが望ましい。また、ガス充てんに際しては機器内部を真空乾燥するた め、真空度０．１３３ｋＰａに達した後、少なくとも３０分以上真空引きし、ＳＦ６ガスを所定の圧力まで充てんしている。

ＳＦ６ガス自身の絶縁強度は、ガス中水分にそれほど影響されない。しかし、ＳＦ６ガ ス中に固体絶縁物が存在すると、絶縁物表面への水分付着によって沿面絶縁特性が影響を受ける。そのため、ガス絶縁機器中においては露点が０℃以下になるよ うに水分量を管理すれば、絶縁低下はほとんど無視できると考えてよい。基本的にはガス中水分の露点は許容値０℃、管理値－５℃以下として実用上支障ない が、実際は濃度表示で第１表（添付）のように定められている。；

ＳＦ６ガス中の水分やアークによる分解ガスＳＦ４、ＳＯＦ２を 管理値以内とするため、両者を吸着する吸着剤がガス絶縁機器内部に封入されている。この吸着剤としては、主に活性アルミナ、合成ゼオライトが用いられてい る。しかし、合成ゼオライトのほうが分解ガス吸着能力及び低温度領域における水分吸着能力とも活性アルミナより優れた特性を有している。

（ｂ）じんあいの管理
ＳＦ６ガスの絶縁特性は平等な電界条件下では優れているが、その反面、金属粉などのじんあいが付着していると大幅に絶縁が低下する危険があるので、据付時におけるじんあいの管理について十分配慮する必要がある。

現 地据付時には、機器内部へじんあいの侵入を防ぐために機器全体を遮へい物で囲み、タンクの開放部もビニルシートなどで覆って作業を行っている。また、作業 者も専用の防じん服、靴および帽子を着用し、人に付いて侵入する異物を防いでいる。据付時のじんあいの管理はダストメータで測定し、２０カウント（０． ２ｍｇ／ｍ＾３）以下であることが望ましい。

ＳＦ６ガスの絶縁性能に顕著な影響を与えるのは０．１ｍｍ以上の金属片であるが、これらは目で十分検知することができ、組立時に除去することが可能である。

一 般的なガス絶縁機器の組立工場におけるじんあいの管理は０．０１～０．０５（ｍｇ／ｍ＾３）程度となっているのに対し、現地据付時はその管理値より１桁悪 い環境で作業するので、十分な環境整備を必要とし、将来的には作業環境に左右されない接続・組立工法、あるいは全装可搬化を図る必要がある。

（ｃ）ＳＦ６ガスの純度管理
ＳＦ６ガスの不純物としては、ＣＦ４、水分、空気、フッ化水素、油分などがあり、微量であれば実用上無視しても支障がないが、ＳＦ６ガスを再利用する場合にガス給装置の取扱によっては水分、油分などが混入するので、ＳＦ６ガスの純度に注意する必要がある。

ＳＦ６ガスの純度管理については、機器に封入したＳＦ６ガスを直接管理するのが望ましいが、ガス給排時のＳＦ６ガス絶縁機器や給排装置の回収タンクの真空度を０．１３３ｋＰＡ以下になるようにすれば問題とならない。

なお、ＳＦ６ガスの純度は第２表に示す値で管理すれば実用上支障はない。

以上、です。久々に長い…。

二種二次試験機械制御過去問、H18問4、補足。

ここの補足、です。
問題分、解答内容については、ここ参照で。

問４
【解説】
閉ループ伝達関数Ｗ（ｓ）の分母を０とおいた式を特性方程式といい、その解を特性根または極という。

本問では特性方程式はｓについての二次方程式であるから、その極は二次方程式の解の公式から求めることができる。

【解説補足】
オリジナル補足を。
（１）
制御系の解析において、伝達関数など…、は、ｓ領域、つまり、ｓ＝ｊωとして、周波数領域では四則演算として扱えるが、これはｔ領域（時間領域）では微積分など、関数計算が必要となる。で、あるため、時間領域からラプラス変換（周波数領域へ）し、四則演算で伝達関数を求めるのが一般的。（１）の問では、答えを時間領域で求める必要があるため、最終的に逆ラプラス変換を行う。
このあたりの計算は、理論一次試験レベル（ただ、三角関数になるケースは滅多にないけど）でも十分いける、と思われます。

（２）は、各要素の入出力、フィードバックを慎重に解いていけば問題なし。

（３）は、図の→側（ＵとＹの関係）が前問と同じである事がまずはポイント。その上で合成の伝達関数を求めれば良い。
極を求めるには、分数の分母＝０、とおけばよい。これは、分母＝０、つまり伝達関数全体が∞となるのが極、だから。
そして、分母はｓの二次式より、二次方程式を解く必要があること、から、ｓは本来二つの値をとる。しかし、問の条件より、極値は一つだけ、より、二次方程式の解の公式中、根号内が０（根号は±の符号を取り、根号内が０でないときにはｓは２値をとるから）の条件が成立する事がわかる。
後は条件を満たす為のｋを求めれば良い。

二種二次試験機械制御過去問、H18問3、補足。

ここの補足、です。
問題分、解答内容については、ここ参照で。

問３
【解説】
昇圧チョッパは、ステップアップコンバータあるいはブーストチョッパなどとも呼ばれる。この昇圧チョッパは、一般に第３図に示す回路構成をとる。

スイッチング素子Ｓがオンのとき（与えられた回路においてスイッチを端子１側に切り替えたことに相当する）、この回路には直流電源→インダクタンス→スイッチング素子Ｓ→直流電源の経路で電流が流れる。このときインダクタンスＬに電磁エネルギーが蓄えられる。

次にスイッチＳがオフすると（与えられた回路においてスイッチを端子２側に切り換えたことに相当する）、直流電源→インダクタンスＬ→ダイオードＤ→負荷抵抗ＲＬおよびコンデンサＣ→直流電源の経路で電流が流れる。このときインダクタンスＬに生じた逆起電力の合成された電圧が加わる。このときの出力電圧Ｖは、電源電圧Ｅより大きくなる。

具体的には設問（３）で導かれた出力電圧Ｖの式においてαは、０≦α≦１の範囲で変化する。したがってαを大きくすると、すなわち、１周期Ｔに対するオン時間ｔｏｎを長くすると、出力電圧が大きくなることが確かめられる。しかし、スイッチング素子がオン（スイッチを端子１に切り換えた時に相当する）のときは、コンデンサＣに蓄えられた電荷が負荷に供給されるだけなので負荷電流が大きいときは、出力電圧の変動が大きくなる。

【指導】
設問（２）は、ｖＬに生じる起電力の方向が、与えられた図に示された起電力の方向と異なることに注意する必要がある。

また設問（３）は、定常状態でインダクタンスＬに蓄えられるエネルギーｗＬ１と放出されるエネルギーｗＬ２が等しくなることに気が付けば解くことができる。

設問（６）は、設問（４）（５）で求めたコンデンサＣに流れる電流ｉＣを用いて、コンデンサＣが充放電に伴って電源から受け取るエネルギーと負荷に与えるエネルギーが定常状態では等しくなることを用いて解く。

以上です。

二種二次試験機械制御過去問、H18問2、補足。

ここの補足、です。
問題分、解答内容については、ここ参照で。

問２
【解説】
変 圧器に生じる負荷損には、銅損と漂遊負荷損とがある。銅損は、変圧器の巻線抵抗によって生じる損失（ジュール損）であり、負荷電流の２条に比例する。一 方、漂遊負荷損は、変圧器巻線の漏れ磁束が巻線及び変圧器を構成するタンクなどの構造物と鎖交したときに流れる渦電流によって生じる負荷損である。

漂遊負荷損のうち、巻線に渦電流が流れることによって発生する損失を巻線内渦電流といい、構造物に渦電流が流れることによって発生する損失を構造物表遊損という。

インピーダンスワットを測定するためには、変圧器の二次側を短絡して一次側に定格周波数の低電圧を加える。このとき、二次側に定格電流が流れるように一次側電圧を調整し、その一次側電圧がインピーダンス電圧であり、入力電力がインピーダンスワットである。

インピーダンスワットは、銅損と漂遊負荷損をあわせた抵抗損に等しい。

変圧器の等価回路の回路定数を求めるために以下に示す試験が行われる。

（１）抵抗測定
変 圧器の巻線に電流を流したとき、巻線の電圧降下を電流で割った値として求める。この方法を直流電圧降下法という。この場合、測定時に流した電流によって巻 線が発熱しないよう、定格電流の１５％を超えない直流電流で測定する。求められた値は次式によって基準温度７５℃における抵抗値Ｒ７５に換算する。

Ｒ７５＝Ｒｔ×（２３４．５＋７５）／（２３４．５＋ｔ）
　　≒Ｒｔ×（２３５＋７５）／（２３５＋ｔ）　（Ω）

ただし、ｔ：測定温度（℃）
Ｒｔ：ｔ（℃）における巻線抵抗値（Ω）

（２）無負荷試験
変圧器の二次側を開放して一次側に電圧計、電流計と電力計を接続する。このｔき定格周波数の定格電圧Ｖ１ｎ（Ｖ）を加え、励磁電流Ｉ０（Ａ）と入力電力Ｐｉ（Ｗ）を測定する。測定した結果から変圧器の励磁コンダクタンスｇ０、励磁アドミタンスＹ０、励磁サセプタンスｂ０がそれぞれ求まる。

ｇ０＝Ｐｉ／Ｖｉｎ^2　（Ｓ）
Ｙ０＝Ｉ０／Ｖ１ｎ　（Ｓ）
ｂ０＝√（Ｙ０^2－ｇ０^2）　（Ｓ）

（３）短絡試験
変圧器の二次側を短絡して、一次側に電圧計、電流計と電力計を接続する。このとき一次側にインピーダンス電圧Ｖｓｎを印加すると定格電流Ｉ１ｎが流れる。インピーダンス電圧Ｖｓｎは定格電圧に比べて数％と低い値なので磁路が飽和しない。このため鉄損を無視することができ、電力計の読みから銅損Ｐｃを測定することができる。このＰｃから一次側に換算した等価抵抗Ｒ１および等価リアクタンスＸ１をそれぞれ求めることができる。

Ｒ１＝Ｒ１＋ａ^2ｒ２＝Ｐｃ／Ｉ１ｎ^2　（Ω）

Ｘ１＝ｘ１＋ａ^2ｘ２
　＝√｛Ｖｓｎ／Ｉ１ｎ）^2－（Ｐｃ／Ｉ１ｎ^2）^2｝

二種二次試験機械制御過去問、H18問1、補足。

ここの補足、です。
問題分、解答内容については、ここ参照で。

問１
【解説】
（１）同期速度と滑り
誘導電動機の極数をｐ、電源周波数をｆ（Ｈｚ）とすると回転磁界の回転速度（同期速度）Ｎｓ（min^-1）は、次式で求まる。

Ｎｓ＝１２０ｆ／ｐ　（min^-1）

回転子は回転磁界と同一方向で同期速度よりやや低い速度で回転する。このとき回転子が切る磁束によって回転子に誘導電流が流れ回転子にトルクが発生する。回転子は、この発生したトルクと負荷のトルクがつり合う速度で回転する。

ｓ＝（Ｎｓ－Ｎ）／Ｎｓ

第１図に示す誘導電動機の１相あたりのＬ形等価回路（簡易等価回路）において、簡単に励磁電流を無視して考えると、一次電流Ｉ１（Ａ）は、

Ｉ１＝Ｖ１／√｛（ｒ１＋ｒ２’／ｓ）^2＋（ｘ１＋ｘ２’）^2｝　（１）

となる。一次巻線の総数をｍとすれば、二次入力Ｐ２（Ｗ）は（１）式を用いて、

Ｐ２＝ｍＩ１^2ｒ２’／ｓ
　＝ｍＶ１^2／｛（ｒ１＋ｒ２’／ｓ）^2＋（ｘ１＋ｘ２’）^2｝　（２）

となる。次に電動機の回転角速度をω（rad/s）、電源の周波数をｆ、極数をｐとすれば、トルクＴ（Ｎ・ｍ）は次式となる。

Ｔ＝Ｐ２／ω
　＝ｐ／４πｆ・ｍＶ１^2／｛（ｒ１＋ｒ２’／ｓ）^2＋（ｘ１＋ｘ２’）^2｝　（３）

（１）～（３）式が示すように二次抵抗とすべりの間にはｒ２’／ｓの関係がある。このため二次抵抗ｒ２をｋ倍したときに、滑りｓがｋ倍になれば元の状態と同じ値が得られる。これを比例推移という。この比例推移を利用することで始動時に必要なトルクや電流の値を調整することができる。

この問題は、全負荷トルクで始動又は運転することが問われているので、回転子巻線を短絡した時の滑りｓｆと回転子巻線抵抗ｒを用いて比例推移の式を立てれば良い。

また回転子巻線および外部抵抗が星型接続であるから、第１図の１相分の等価回路から求めることができる。

二種二次試験過去問、H18問6、補足。

ここの補足、です。
問題分、解答内容については、ここ参照で。

問６
【解説】
（１）保護協調
保護協調とは、ある系統およびある機器に万一事故が発生した場合、故障発生源を早期に検出し、迅速に除去し、事故の波及・拡大を防ぎ、健全回路の不要遮断を避けることにある。

したがって、保護装置がばらばらに動作すると、故障した部位が正確に選択に選択できず、不必要に広範囲の停電を引き起こす場合がある。このため、各保護装置相互間の適正な協調が必要となる。

一 般に地絡保護については、需要家変圧器一次側は、電力会社接地系に属するので、保護継電器方式の協調が必要であり、継電器の動作電流値などについて、十分 協議する必要がある。なお、変圧器二次側の需要家構内系統は、変圧器により電力会社系統と接地系が分離しているので、任意の系統接地方式・保護継電方式を 選定する事ができる。

問題の事故点は事故がＡ需要家変圧器の一次側となっているので、供給用変電所の接地系に属するため、電力会社接地系に属するので、この場合、保護継電方式の協調が必要である。

なお、一般電気事業者は受電点継電器の整定に対し、第１表（添付図）に示す値を基準としている。

また地絡協調については、第１表によれば完全地絡時に０．２秒以下となっているが、本問の場合は、問題の設定条件から第１図（添付図）に示すように、上位～下位設備間の動作時間を制定する。

（２）ＣＴの接続
通常、三相回路では各相にＣＴを設け、二次側を星型に接続し、短絡検出は各ＣＴ二次回路を、地絡検出は残留回路を利用して行われる。

したがって、これらのＣＴ特性が同一でないと、三相合成電流の誤差分としての残留電流が通常状態でも流れる事になり、継電器の誤動作を招くおそれがある。ＣＴの変流比が大きい場合の残留回路利用は、継電器入力が小さくなるので必要に応じて三次巻線付ＣＴを使用する。

第２図に地絡検出ＣＴ結線図を示す。

また、地絡状態を除けば回路電流ベクトル和は零であることを利用して、２ＣＴによる計測および短絡保護を行うことができる。これも、ＣＴ特性が同一であることが前提である。

二種二次試験過去問、H18問5、補足

補足

ここの補足、です。
問題分解答内容については、ここ参照で。

問５
【解説】
連系系統の周波数と連系線の電力変化の基本を十分理解しておけば、特に複雑な計算を行う必要はない。

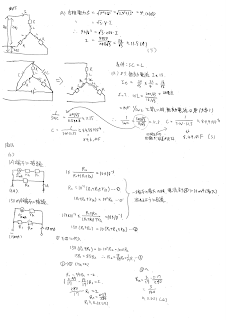
ここでは、第１図（手書最下部左）のような二つの連系系統の周波数変化ΔＦと連系線潮流変化ΔＰＴを求めてみよう。

（１）Ａ系統で電力変化ΔＰＡがあった場合
第２図（ａ）（手書最下部中）のようにＡ系統で電力変化ΔＰＡ（発電力ΔＧＡ－負荷変化ΔＬＡ）があったとき、Ａ，Ｂの系統容量及び系統定数をそれぞれＰＡ[ＭＷ]、ＫＡ[p.u.（ＭＷ）／Ｈｚ] およびＰＢ[ＭＷ]、ＫＢ[p.u.（ＭＷ）／Ｈｚ] とすれば、両系統の周波数変化ΔＦ’[Ｈｚ] と連系線の潮流変化ΔＰＴ’[ＭＷ] は、次のようにして求められる。

ＰＡ－ΔＰＴ’＝ＫＡＰＡΔＦ’　（電力変化分＝変化定数×系統周波数変化）
ΔＰＴ’＝ＫＢＰＢΔＦ’　　（潮流変化分＝相手の変化定数×系統周波数変化）

∴ΔＦ’＝ΔＰＡ／（ＫＡＰＡ＋ＫＢＰＢ）
∴ΔＰＴ’＝ＫＢＰＢΔＦ’＝ＫＢＰＢ／（ＫＡＰＡ＋ＫＢＰＢ） ×ΔＰＡ

（２）Ｂ系統で電力変化ΔＰＢがあった場合
第２図（ｂ）（手書最下部右）のようにＢ系統で電力変化ΔＰＢ（発電力ΔＧＢ－負荷変化ΔＬＢ）があったときには、（１）と同様にして両系統の周波数変化ΔＦ''[Ｈｚ] と連系線の潮流変化ΔＰＴ''[ＭＷ] を求められるが、方程式を立てるとき連系線潮流の向きが（１）と逆向きになることに注意することが大切である。

ＰＢ－（－ΔＰＴ''）＝ＫＢＰＢΔＦ''
ΔＰＴ''＝－ＫＡＰＡΔＦ''

∴ΔＦ''＝ΔＰＢ／（ＫＡＰＡ＋ＫＢＰＢ）
∴ΔＰＴ''＝－ＫＡＰＡΔＦ''＝－ＫＡＰＡ／（ＫＡＰＡ＋ＫＢＰＢ） ×ΔＰＢ

（３）両系統で同時に電力変化があった場合
実際の電力系統では、Ａ，Ｂ系統で同時に電力変化が生じており、そのときの系統周波数変化ΔＦおよび連系線の潮流変化ΔＰＴは、Ａ，Ｂ系統単独の電力変化時の和となるので、

ΔＦ＝ΔＦ’＋ΔＦ''＝（ΔＰＡ＋ΔＰＢ）／（ＫＡＰＡ＋ＫＢＰＢ）
ΔＰＴ＝ΔＰＴ’＋ΔＰＴ''＝（ＫＢＰＢΔＰＡ－ＫＡＰＡΔＰＢ）／（ＫＡＰＡ＋ＫＢＰＢ）

以上です。

二種二次試験過去問、H18問4補足

ここの補足、です。
問題分解答内容については、ここ参照で。

問４
【別解】
重ね合わせの理によって、Ａ系統のみの端末負荷があると考え、Ａ系統端末負荷の電流ＩＡによる開閉点を流れる電流ＩＡ’をもとめる。

ＩＡ’＝ＩＡ×ＺＡ／（ＺＡ＋ＺＢ）…分流（？）

計算すると、

ＩＡ’＝７３．０２＋ｊ３４．９８７

同様にＢ系統のみの端末負荷があると考えた場合、ＩＢによる開閉点を流れる電流ＩＢ’は、

ＩＢ’＝ＩＢ×ＺＢ／（ＺＡ＋ＺＢ）

計算すると、

ＩＢ’＝３０．２５１－ｊ１４．３９５

したがって、連系点に流れるループ電流Ｉの大きさは、ＩＡ’とＩＢ’を重ね合わせたものとなるので、
（ループ電流の向きより、ＩＢ’はＩと逆向き→符号が負）

Ｉ＝ＩＡ’－ＩＢ＝４２－７６９＋ｊ４９．３８２

となり、キルヒホッフで解いた値と一致する。

【解説】
消費電力に変化が無いこと、がポイントでしょうか。
消費電力に変化が無く、非連系→連系とした場合に、ループ電流が流れる、と。なんだか不思議な感じがしますが…。起電力がないループ回路に、電流が流れる、って…。

ちゃんと調べてみたわけじゃないですが、多分無効電力、有効電力のやりとりが行われた結果、負荷には変化が無い、って事かな？
（いや、逆か。負荷に変化がないために、有効電力・無効電力のやりとりが発生し、ループ電流が流れるのかな）

そのあたりの考え方はちょっと難しいですが、解法自体はしっかりやればそこまででもないと思われます。
手書図（解等の方）が思い浮かび、起電力が０で、とかが浮かべば、後はミスに注意して解くだけですから…。

以上

二種二次試験過去問、H18問3補足

ここの補足、です。
問題分解答内容については、ここ参照で。

問３
【解説】
送電線と通信線が接近しているとき、相互の誘導的結合によって、通信線に電圧が誘起される現象を電磁誘導といい、通常、高電圧の三相送電線は故障以外はほとんどバランスして相電流が流れているので、大電流が流れてもある程度通信線が離れていると、各相と通信線の間の相互インピーダンスはほとんど等しく、電磁誘導電圧は生じない。

しかし、送電線に地絡が発生して過大な電流が流れると、その大地を帰路とする電流成分による電磁誘導作用によって、通信線に大きな電磁誘導電圧を生じ、通信線の作業員に危害を加えたり、通信機器を破壊するなどの傷害を与えるおそれがある。

（１）異常時誘導電圧（１線地絡故障）の求め方
送電線に１線地絡故障が発生した時に、電磁誘導により通信線に発生する誘導電圧Ｖｍ（Ｖ）を表す式は、次のように求めることができる。

電磁誘導障害は第２図のように原理的には相互インピーダンスをもつ電気回路で考えられ、閉回路の相互交さ磁束によって生ずる。

したがって、第２図のように、Ｉｅ、Φ、ｅの正方向を決めれば、通信線に生じる単位長あたりの誘導電圧は、

ｅ＝ｄΦ／ｄｔ

ここで両導体間の相互インダクタンスをＭ（Ｈ／ｍ）とすると、Ｍｉ＝Ｎφ→φ＝Ｍｉ／Ｎを代入し、

ｅ＝ｄφ／ｄｔ＝Ｍ（ｄｉ／ｄｔ）

これにｉ＝Ｉｅ ｓｉｎ ωｔ を代入して、

ｅ＝Ｍ・ｄ（Ｉｅ ｓｉｎ ωｔ）／ｄｔ＝ωＭＩｅｃｏｓωｔ　（Ｖ）

次にＤ（ｍ）を乗じ絶対値を求める。

Ｖｍ＝|ｊωＭＩｅＤ|
　　＝２πｆＭＩｅＤ　（Ｖ）

が求まる。また、三相送電線を考えると、各相の電線と通信線間の相互インダクタンスの相違を無視して、第３図のように、Ｍａ≒Ｍｂ≒Ｍｃ≒Ｍとすると、

Ｖｍ＝ｊ２πｆＭＤ（Ｉａ＋Ｉｂ＋Ｉｃ）
　　＝ｊ２πｆＭＤ×３Ｉ０　（Ｖ）

で表される。ただし、上式のＩ０は、零相電流を表す。

したがって、上式より電磁誘導は送電線の零相電流によって誘起されることがわかる。

二種二次試験過去問、H18問2補足

ここの補足です。

問２
【解説】
（１）移動用変電設備
事故によって変電所機器が損傷した場合、支障なく電力を供給するために、いくつかの変電所の共通予備として使用する設備で、変電所機器の点検・修理などで比較的長期に停止する場合や工事用としても有効である。

（ａ）移動用変圧器
２２／６，３（ｋＶ）、３，６（ＭＶ・Ａ）、または６６（７７）／６，３（ｋＶ）、３，６，１０（ＭＶ・Ａ）、あるいは１５４／６，３（ｋＶ）、１０（ＭＶ・Ａ）などの定格の配電用変圧器が各電力会社の設備実態に応じて設置されている。

これらはトラックまたはトレーラに積載したまま移動使用可能で、１０（ＭＶ・Ａ）以上の比較的大きな変圧器もトラック積載可能である。一部には１５４／６６（ｋＶ）、３０（ＭＶ・Ａ）程度の送電用変圧器もある。

（ｂ）移動用ケーブル
１５４（ｋＶ）以下の移動用ケーブルが各電力会社の設備実態に応じて設置されている。

以上です。

２種二次試験の勉強に突入。過去問より、１問ずつ〜解説です。

平成１８年電力管理　問１
ここの補足・解説です。

【解説】
（１）水車の適用有効落差領域と主な特徴を以下に示す。
（ａ）ペルトン水車
ペ ルトン水車は、水の位置エネルギーを運動エネルギーに変えて機械的エネルギーを得ているため、一般に１５０m程度以上の高落差領域で用いられる。最高効率 は他の水車に比べてやや劣るが、ペルトン水車は負荷変動時にニードル弁で水流を調節するため、軽負荷時でも効率の低下が少なく、負荷の変化に対して効率特 性は平坦である。なお、多ノズル形では負荷に応じてしようノズル数を切り替えて運転することにより、さらに効率の低下を防ぐことができる。

（ｂ）フランシス水車
最も数多く、一般的に採用されている型式であり、５０〜５００m程度の中落差から高落差まで広範囲にわたって適用される。
最高効率は定格出力においては高いが、効率特性は負荷の変化及び落差の変化に対して敏感であるため、軽負荷時には効率がかなり低下する。

（ｃ）斜流水車
一般に４０〜１８０m程度の中落差領域で用いられる。フランシス型より高比速度であるから、主機全体としては経済性をはかることができる。
構造上はフランシス水車に似ているが、プロペラ水車の羽を斜めにして、ランナボスの径を大きくしたものと考えることもでき、適用領域と効率特性は、フランシス水車とプロペラ水車の中間にある。
デリア水車では負荷に応じてランナベーンの開度を調整することにより負荷の変化に対して平坦な効率特性が得られる。

（ｄ）プロペラ水車
２０〜８０程度の低落差から中落差領域で用いられる。比速度は高く、固定羽式では低負荷時に効率が著しく低下するが、ランナベーンを可動としてカプラン水車では、負荷の変化に対して平坦な効率特性が得られる。

（ｅ）その他
さらに低落差領域では、バルブ水車、チューブラ水車が用いられ、数百ｋＷ以下の領域では、構造の簡単なクロスフロー水車が用いられる。

（２）水車の比速度
水 車の比速度とは、その水車と相似な水車を仮想して、１mの落差のもとで相似な状態で運転させ１ｋＷの出力を発生するような寸法とした時の、その仮想水車の 回転速度をいう。すなわち、比速度が高いものは、高速回転形となり、ランナ形状が小型となる。ただし、比速度は下記に示されるように与えられた落差から上 限が決められる。ペルトン水車は比速度の範囲が狭く低速度形となるため、水車、発電機とも大型になる。

種類…比速度（m・kW）…適用落差（m）
ペルトン水車…Ns≦4300/（H＋195） ＋13…150〜800
フランシス水車…Ns≦21000/（H＋25） ＋35…40〜150
斜流水車…Ns≦20000/（H＋20） ＋40…40〜180
プロペラ水車…Ns≦21000/（H＋20） ＋35…5〜80
クロスフロー水車…90≦Ns≦110

水車は落差、出力によって適用範囲が分けられるが、適用できる型式が二つ以上ある場合には、効率特性、コストなどを総合勘案して決定する。
ま た、水車の最高効率は比速度Nsと出力により図（後日）のような傾向を示す。次図は出力と効率の関係を示す。ペルトン水車ではノズル数を変えることにより 低負荷時の効率低下を防ぐことができる。カプラン水車ではランナベーンの角度を変えることにより負荷の変化に対して平坦な効率特性が得られる。

（３）水車の回転速度
水 車及びそれにつながる発電機は回転速度が大きい程寸法が小さくなり、価格も安くなる。しかし、回転速度があまり大きいと、機械的な強度から制約を受ける。 また、キャビテーションが発生しやすくなり、効率の低下及びランナ壊食などの問題が起きる。したがって、水車には適当な回転速度がある。

07年3種機械の解答編（問11～18）の補足。

ここの補足です。

問１１
立体角の考え方がわかればＯＫ、かな。
添付の図を参照してみてください。
弧度法と対応させると、半径ｒに対し円周2πｒとの比が中心の角度としての弧度法。
これに対し、半径ｒに対し、全表面積が４πr＾２。
r＝１の時で比率を考えればよい。
よって、立体角／４πで、テーブル面に対応する放射面積（光束の有効分）が求められる。
後は、テーブルへの全光束を面積で除すれば照度。

問１２
本番ではちゃんと読んでなく、光電効果の所を間違えてしまった…。
（光が３乗に比例か４乗に比例か自信がなかったので…）
あとは、ゼーベック効果と、その逆（起電力によって熱）のペルチェ効果、あわせて覚えておくとよいかも。　（１）

問１３
ファラデー定数はＣ／ｍｏｌ。電流Ｉは、Ｃ／ｓで表す事ができる。
よって、ファラデー定数を３６００（秒）で除すれば（Ｃ／ｓ）／ｍｏｌ
となり、２６．８（Ａｈ／ｍｏｌ）である。
発生電気量は、
２６．８×（ｘ／６５．４）×２＝２×５×０．６５

これよりｘを解けば良い。　（４）

問１４
左上から１〜４と付けると、１はＡ・Ｂ。２はＡ・Ｂ。
４は２が１の時のみ、つまりＡとＢが共に１のときのみ０を出力し、Ａ、Ｂ一方が０の場合には１が入力される。また、３は、Ａ、Ｂ共に１の時には入力の一方（１の出力）が常に０であり、３は１を出力する。
このように考えていくと、結果的に出力Ｘ＝Ａ・Ｂとなる。　（３）

問１５
（ａ）は問題なし。
（ｂ）まず、電機子抵抗を無視→ｒ＋ｊｘの同期インピーダンスのうち、rが無視できる。よって同期インピーダンス|Ｚ|＝ｘであり、誘導性なので角度は９０°。
これより、電機子電流は４４０／３．５２＝１２５（Ａ）
Ｐ＝ＥＩｃｏｓ（δ—θ）であり、δは上記の通り９０°。θは負荷の力率角。
これらより、
Ｐ＝ＥＩｃｏｓ（９０—θ）＝ＥＩｓｉｎ（θ）
よって、トルクＴ＝Ｐ／ωで求める。

問１６
普通に解けば（ａ）はOK。
（ｂ）は、多分絶対値は変わらない、とかだと思うんですが…。
（１）は、なんとなくそうですね。
（２）は電力とか勉強すれば出てきます。
（３）式を見れば、雰囲気そうなりますね。
（５）３調波が多いのは常識ですね。
と、消去法でもいいかも。ま、間違えましたけど。

問１７
普通にインピーダンスとして、R＋１／（jωC）であり、この分圧（のコンデンサ側）の電圧、これが伝達関数となる。（ａ）、（ｂ）共に同様である。

問１８
ユニポーラコード：ビット全ての分解能を０〜ＦＦＦに割り当てる方法。—側はとれない。
オフセット・バイナリコード：８００を起点（０）とし、０〜８００（０）〜ＦＦＦで±に範囲をとる。
つまり、—側が８００（１６進）、＋側が７ＦＦ（１６進）の範囲で値をとる
バイポーラ・コード：出力０を８００（１６進）とする所は同じであるが、８００の点で入力の±が反転する。例えば、力率のように＋１００％と—１００％がデータ的に隣にあるほうがアナログデータの都合が良い場合などに用いられる（んだと思う）。–側を求めるときには、中心としての８００（１６進）との差、及び幅としての８００（１６進）との差、和を考えなければならない事に注意。

07年3種機械の解答編（問1～10）の補足。

ここの補足、です。
問題分解答内容については、ここ参照で。

問１～１０です。簡単に、解説。

問１
直流直巻発電機は、界磁巻線が電機子巻線と直列に接続してある方法である。つまり、電機子電流＝界磁電流、と考える事ができる。電機子電流は負荷に応じて増減する。また、界磁電流が弱まる→界磁が弱まる→回転子を拘束する力が弱まる、と考える事ができ、回転速度としては上昇する方向。
以上を総合して考えると、無負荷→電機子電流小→界磁電流小→界磁小→回転速度大　で、極端な場合は危険となる。

問２
発電機が無負荷という事は、電機子電流Ｉａ＝０。つまり、電機子での電圧降下はなく、端子電圧＝電機子電圧と見る事ができる。端子電圧と回転数の比は等しいことから、算出できる。

問３
巻線形三相誘導機は、回転磁界を作る固定子と、回転する巻線を持つ、回転子から成る…。
本問では、５つの項目を埋める問題でしたが、選択肢的に自信があったのが、回転磁界、ガラス巻線、始動特性、の３項。これでも、解答には辿り着く事ができるため、慎重に答えを選びましょう。

問４
６極６６Ｈｚの同期速度Ｎｓは
Ｎｓ＝１２ｆ／Ｐ（ｆ：周波数、Ｐ：極数）
また、滑りｓの時、回転速度Ｎは
Ｎ＝（１－ｓ）Ｎｓ
から算出可能。注意はＶ／ｆ一定など、関係ない言葉が入っているところ。
（実際にはこれがないと周波数に比例する、とはいえないので関係なくはないが、算出には関係なし）

問５
同期インピーダンスは、短絡電流を発生させる端子電圧の１／√３を、短絡電流で除したもの。ここで、端子電圧は励磁電流に比例するので、励磁電流が９６／４８０＝１／５なので、端子電圧は４８０Ａ時（無負荷時）の１／５。後は与えられた短絡電流と短絡時の端子電圧から算出すればよい。

問６
負荷の容量は皮相電力でＳ＝１００／０．７５＝１００×４／３
自己容量は、巻線Ｎ１（６６００－６０００の短い巻線部の容量）を指すため、
Ｓを６６００：６００の比でわけた、６００相当分が自己容量となる。

問７
インピーダンスの大きさ|Ｚ|は、電圧／電流。また、皮相電力Ｓは電圧×電流、有効電力Ｐは問より与えられ、よって、力率はＰ／Ｓで計算できる。
変圧器の１次巻線抵抗分をｒ、リアクタンス分をｘとすると、
|Ｚ|＝√（ｒ＾２＋ｘ＾２）
ｃｏｓφ＝ｒ／|Ｚ|
と表現する事もできるため、これらを連立させて解けばよい。

問８
遮断器、断路器の違い、昔は油遮断器が主流であったが、メンテ性や防火の面から低めの高圧で真空遮断器（ＰＡＳとかですね）、高めの特高とかでＳＦ６ガスの入り遮断器などｔ使用される。

問９
ポイントは、全波整流回路を平滑して方形波を作っているところ。さらに、位相が微妙にずれている所。多分、後、波高値もかな？これらから該当するものを選べばＯＫ。

問１０
ＣＶＣＦの問題です。ＣＶＣＦは定電圧定周波数装置の事で、交流のバックアップ電源に用いられます。ＵＰＳと同義に言われることもある。（本来はＵＰＳはＣＶＣＦだけど、ＣＶＣＦはＵＰＳとは限らないはず：周波数制御の有無とかの話で）つまり、コンピュータなど、瞬時停電にも弱い機器（正常に終了しないとソフト・ハード的に故障の恐れのある機器や停電時でも監視したい制御・表示機器など…）を、常用の交流電源と非常用のバッテリによる電源とを、無停電にて自動切換えし、電源断とならないようにする機器。で、あると共に、交流入力をインバータを通す事で定電圧・定周波数として出力する機器。

以上です。明日はこの続き、かな？

07年3種理論の解答編の補足。（問11～18）

ここの補足、です。
問題分解答内容については、ここ参照で。

問１１
ａ．可変容量ダイオード→ｐｎ接合に逆バイアスをかける事で空乏層幅をコントロールし、容量可変（だったはず）
ｂ．定電圧ダイオード（ツェナダイオード）→ｐｎ接合に逆方向バイアスを一定以上印加した場合におこる、降服現象時にダイオード電圧はほぼ一定となるという性質を利用したもの。
ｃ．レーザダイオード→ｐｎ接合に順バイアスをかける
（５）

問１２
演算増幅器は、直流回路でももちろん用いられ、＋端子と－端子の入力電圧の差分に対して増幅動作をふる素子である。

問１３
電子の等速円運動。これについては各式を覚えるか、導出するしかない。導出は、短く言うと…、
円運動→遠心力と求心力が平衡。
遠心力は電荷の重さ×加速度（Ｆ＝ｍａ：運動方程式）
求心力は磁界中の電磁力で、Ｂｅｖ（磁界×電荷×速度）
ここで、速度は位置の微分、加速度は速度の微分、これらをｘ軸成分、ｙ軸成分に分け（三角関数）で、つりあう、と式を立てる。これを解くと円の方程式が求まり、半径も求められる。さらに、半径や速度から周期が求められる。
詳細はこちら（多分２種レベル？）

問１４
図１は、電流に電圧計計器誤差を含む。図２は電圧に電流計計器誤差を含む。計算の詳細は手書参照。

問１５
詳細は手書参照。ポイントはΔ－Ｙ変換。

問１６
可動コイル→電磁力を利用するし、電磁力は電流に比例。（ｂ）については手書参照、だが、端子の最大電流と電流計に流れる最大電流を対応させ、分流でどちらの時にも電流計最大電流が流れる抵抗値を連立方程式から求める。

問１７
単位で考える。電子個数ｎは個／ｍ、電荷ｅはＣ／個、移動速度ｖはｍ／ｓ、電流ＩはＡ（＝Ｃ／ｓ）。これらから、Ｉ＝ｎｅｖ。よって、ｖ＝Ｉ／ｎｅで求める。
（ｂ）については、ｎ、ｅは定数。導線の抵抗値は、２倍になると、２乗に反比例する抵抗値（面積に反比例だから）は１／４。本来、１０Ａ×４＝４０Ａになる所を、３０Ａにしかなっていない、つまり、通過電子数が３／４しかないことになる。

問１８
よくわかりません（考えてない…）。
気が向いたら考えて見ますが、多分向きません…。

07年3種理論の解答編の補足。

ここの補足です。

問１
直線導体：H=Ｉ／２πｒ　円形導体の中心磁界：Ｈ＝Ｉ／２ａ　から算出

問２
通常の磁性体→比透磁率は１以上で、常磁性体、逆向きだと比透磁率＜１で、反磁性体。強磁性体は鉄やニッケル。磁界中で磁性物質が磁化されるのは、磁気誘導。

問３
電気力線はＱ／ε　本。電気力線は＋電荷から出て－電荷へ入る。

問４
図１：Ｃ１＝２Ｃ／３、Ｃ２＝３Ｃで、エネルギーは1/2・ＣＶ＾２。これらから変形し、分圧なども使って解く。

問５
回路の合成抵抗からＲ２の電流を求め、エネルギー（電力）をＲ２ｉ２＾２で求める。これが最大になる条件は分母が最小。このためには、分母の変数を含む項同士を掛けたら一定となる時、双方の項が等しい、という条件となる。

問６
平衡条件は向かい合う抵抗の積同士が等しい場合。また、この時単純な並列回路としてみればよいので、電流も求められる。

問７
コンデンサが消費したエネルギーが抵抗で消費するエネルギー。

問８
周波数が１／２→コンデンサのインピーダンスは２倍。ここから求める。

問９
並列なので、それぞれ電圧は同じ。周波数ももちろん同じ。電流はインピーダンスの逆数に比例、から求める。（インピーダンスがωＣと１／ωＬ）

問１０
時定数はＲＣ。なので、回路の合成抵抗と合成容量を図１～５について求め、ＲＣを考えたらＯＫ。

以上です。
問題はどっかから入手してくださいね。

07年種法規問６，７、の補足。

ここの補足です。

問６　高圧需要家の電力需要設備
一つの変圧器に、三つの負荷が接続されており、年間使用電力量、最大電力、年負荷率のうち二つが与えられた時に、残りの一つを求める問題。
（１）～（３）
負荷率＝平均電力／最大電力
であり、年負荷率で考える。平均電力＝電力量／時間、なので、年間電力量を（３６５日×２４時間）で除すれば、年間の平均電力が算出される（電力量はＭＷ、電力はｋＷなので、単位を換算し忘れないこと）。

（４）
不等率は、負荷の最大電力の和／系統の最大需要電力　で求められる。ようは、負荷単位での最大電力が同時に集中するとは限らない、という事も含め、実際変圧器で見た最大需要電力≠負荷の最大電力合計となる。この比が不等率。

よって、（１）～（３）で求めた最大電力を合算し、それを不等率で除算すれば、トータルの最大需要電力が算出できる。

（５）
利用率とは、最大需要電力／定格なので、（４）が算出されれば計算できる。

なんとなく、覚えてたけど、言葉から推測しても解けるかもしれませんね。

問７　架空電線の着氷雪害
送電線への着氷雪害に関して。ギャロッピングは配電線に雪や氷が付着し、それが翼状になって風を受けると揚力を受ける、という現象。着氷雪が考えられる事の他、風が強い、など気象・地形他の条件・要因が重なって発生する。

自励振動が起こる→振動周期と、揚力とが、同調したら振幅がどんどん大きくなる、って事だと思われます。

防止策としては、振動しても送電線同士が接触しない対策、ということになります。

07年種法規問３，４，５、の補足。

ここの補足です。

問３　高圧配電線との連系
冷静に考えればそんなに問題なし、の問題です。
ａ．について
一般電気事業者、卸電気事業者、つまり、電力会社等と考え、そこと高圧で連系し、かつ、自家発電をもっている場合。自家発電があることを前提に受電用配線などが設計されている場合が多い。逆に言うと、自家発電が脱落した場合には配電線等が過負荷になると、配電線過熱等、問題がおこる。そのため、構内の負荷を制限しなければならない、と。
例えば、配電線容量が500A。構内負荷の合計が1000Aで、構内発電が800Aの場合、
通常は500Aしか受電していない（配電線には流れていない）。ここで、発電機が脱落すると、発電分800Aも配電線にかかり、合計1300Aの電流が流れ、危険である。そのため、構内負荷を300A（以上）制限する必要がある、という事です。

ｂ．について
系統に負荷を連系する→並列に負荷が繋がる形なので、電源から見た負荷のインピーダンスは小さくなる、可能性がある（増設分のインピーダンスにもよるけど）。なので、負荷の短絡容量が電源側（電力会社側）などの電線の瞬時許容電流や遮断器の遮断容量を超える短絡電流が流れるような値となると、危険（遮断できない）。そこで、事故電流を制限する措置が必要、という問題。

問４　油入変圧器の劣化診断方法で、油中ガス分析
これは、ちょっと職務の経験上、覚えていたのでラッキーでした。内部異常（アークの発生とか？）によって、絶縁油が化学変化を起こし、異常なガスが発生するので、このガス濃度測定によって劣化傾向を知る方法。

このガスとしては、アセチレンやエチレンがある（この、アセチレンを覚えてて、ラッキー！）。また、この数値に異常があった場合には、さらに精密な診断を行うよ，と言う話。

後は密閉型の場合には空気（外気）の侵入を測定する、として、窒素濃度の測定も劣化診断には有効である、と。

問５　電気工作物の維持
良くある問題。
ただ、このｃ．、ｄ．はよく知りませんでした。なので、（５）は間違えたけど…。この文章は多分良く出るので、他の場所が穴になった場合でも答えられるようにしなければならないです。
例えば、

一　事業用電気工作物は、人体(2)に危害を及ぼし、又は物件に損傷を与えないようにすること。

の文章で、「人体」部分が穴になってましたが、「物件」が穴になってる場合もありました。
他にも、そんな感じでありませうので、注意は必要。

後は、覚えるしかないし…。

とりあえず、以上です。

07年種法規問１、２、の補足。

ここの補足。

今度は法規シリーズです。２問。

問１　電気工事士法及びその関連による、電気工事に該当しない軽微な工事及び電気工事士でなければ従事することができない一般用電気工作物に係る電気工事に作業

ａ．電気工事に該当しない工事
本番では間違えたんですが…、
・電圧６００Ｖ以下→低圧の機器でである事
・スイッチ類に配線を接続（コネクタ系を含む）
・ただし、配線器具の工事を除く
・電鈴やインターホーン、他に使用する小型変圧器で、二次電圧が３６Ｖ以下のものの配線工事。

ｂ．電気工事士でなければ従事する事ができない一般用電気工作物に係る電気工事
・電線類が造営物を貫通する部分に防護装置を取り付ける作業
・金属製の電線管類又はこれらの付属品を建造物の金属張りなどの部分に取り付ける作業

ん～、よくわからない。覚えるしかない類かも。

問２　架空電線等の高さに関する記述
ａ．架空電線類は接触や誘導作用による感電のおそれがないようにしなければいけない。
接触はもちろん、高圧・特高では、ケーブルが非接地だと誘導による感電もあり得るので注意。
もちろん、交通にも支障はだめ。

他はなんとなく常識的に考えればＯＫ。
ｂ．の、表については数値を覚えなければいけませんが、本問で埋めるのは数値２箇所。
で、（２）、（３）は文面より（２）＞（３）。また、文面より（２）＜５．５。
つまり、括弧書きに条件が緩和または強化される要因が書いてあるので、
そこから推察すればＯＫ，かな。

氷雪の多い…、は、電線は積雪上の高さ、です。

以上。補足ってほどでもありませんね。

07年種理論問７，８。の補足。

ここの補足です。

問７
（１）～（５）
ちょっとイレギュラーな考え方かもしれませんが、単位で考えればＯＫ、です。

密度ｐ、ｎ：ｍ＾－３
電荷ｑ：ｃ
電界Ｅ：Ｖ／ｍ
電流：Ａ→ｃ／ｓ
電流密度Ｊ：Ａ／ｍ＾２

電流密度ＪをｑｐμｐＥとすると（問題の通り）、移動度μｐは、
μｐ＝Ｊ／（ｐｑＥ）　（正孔の場合。電子でも同様）
この単位は、
Ａ／ｍ＾２・（ｍ＾－３・ｃ・Ｖ／ｍ）＾－１
→ｃ・ｓ＾－１・ｍ＾－２・ｍ＾３・ｃ＾－１・Ｖ＾－１・ｍ
→ｃ・ｃ＾－１・ｍ＾（－２＋１＋３）・（Ｖｓ）＾－１
→ｍ＾２／Ｖｓ
また、移動度の定義を考えると、速度ｖと電界Ｅの比例定数だから、
ｖ＝μＥ。速度ｖ：ｍ／ｓだから、
μ＝ｖ／Ｅの単位は、
ｍ／ｓ／（Ｖ／ｍ）→ｍ＾２／Ｖｓ

となり、双方は合致する。
また、電子と正孔が同じ電界（電荷）で、同時に動き、
その方向が逆で、電荷も逆なので、電流としては和算でよい。

導電率γは抵抗率の逆数であり、その単位は、
Ωｍ。ΩはＶ／Ａと表現できるので、導電率の単位は、
Ａ／Ｖｍ

よって、電流密度Ａ／ｍ＾２を電界Ｖ／ｍで除すれば、導電率γとなる事がわかる。
（ｑμｎ→ｃ・ｍ＾２／Ｖｓ・ｍ＾－３→ｃ／ｓＶｍ→Ａ／Ｖｍで、導電率はｑμｎで表現できる、ともいえる）

問８
これは、試験時やってない（選択問題なので）し、今ちらっとやってもよくわかりませんでしたが…。

（１）ＩＡ≫ＩＢより、Ｖｃｃに対し、ＩＢを無視する事ができる。この時、ＶＢはＶｃｃの、ＲＡとＲＢによる分圧と考えればよい。

（２）ＩＥ＝（ＶＢ－ＶＢＥ）／ＲＥより（１）で求めたＶＢ，問で与えられたＶＢＥ，ＲＥから解くことができる。

（３）～（５）
コンデンサは交流に対し短絡、と考える。この時、ｖ０１、ｖ０２には、そのまま電圧が出る。
（抵抗分の電圧が）ただし、符号はｖ０２は逆転するので、位相は１８０度。
（負荷特性曲線から導くようですが、覚えておかなきゃ解けない？）

ただ、この問題に関して、直感的には。
トランジスタのベース側に対しそこを基に考えると、接地側に向けてｖ０１、電源側に向けてｖ０２をとっている。ここで、コンデンサによって電圧位相は９０度ずれるが、この考えにより、ｖ０１は進み、ｖ０２は遅れの９０度、になるとするとｖ０１～ｖ０２の電圧位相は１８０度となる。

多分、大きくは外れてないと思うけど…。
後、ｖ０１、ｖ０２が共に入力に対して１倍になるのは、ＲＣとＲＥの抵抗値が同じだから、だと思いますが、その辺を証明する手立ても見つからなきゃ、思いつきもしません。

まぁ、雰囲気的には解答の選択肢から、こうなるんだろうなぁ、とは考えられますが…。


煮え切らないけど、理論編、終了！

07年種理論問６、の補足。

ここの補足、です。
問題分解答内容については、ここ参照で。


各解答（１）～（５）については以下です。
もっと簡単な方法があるのかもしれませんが、計算が大変でした。本番では時間が無く、断念。どっちみち考え方が多少違ってましたが…。計算過程については添付の手書き、２枚目の画像を参照してください。

（１）
Ｐ１，Ｐ３のインピーダンスをＺｘ、Ｐ１，Ｐ２のインピーダンスをＺｄとすると、電圧ｖは、

Ｚｘ／｛Ｚｘ＋（Ｚｄ－Ｚｘ｝＝Ｚｘ／Ｚｄ

に比例する。（分圧）
この式より、ｖは右肩上がり（Ｚｄは定数、Ｚｘは距離ｘに対して右肩上がりのため）となる。
ただし、Ｐ３がＰ１，Ｐ２に極近くない位置では、インピーダンスはほぼＰ１，Ｐ２の接地抵抗分のみ（つまり定数）と考えられ、その分圧による電圧ｖも一定となる。これは、この部分において大地の静電容量は∞となり、交流に対しインピーダンス１／ωＣは０となるから、である。
※この解釈については後で解答を見てから自分なりに納得できる考えはこう、って考えたものなので１００％の自信はないです。本番では右肩上がりの直線を選択しましたし。

（２）
この問について、ブリッジ回路で表すと手書きの図３に表すブリッジ回路において、Ａ＝ＲＫ、Ｂ＝ＲＷ、Ｃ＝Ｒ１＋Ｒ２、Ｄ＝ＲＱとした場合と等価である。これより、平衡条件ＡＣ＝ＢＤから、導出する事ができる。

（３）
同様に、図３においてＡ＝ＲＫ＋ＲＢ、Ｂ＝ＲＷ－ＲＢ、Ｃ＝Ｒ２、Ｄ＝Ｒ１＋ＲＱとした場合と等価。ここで、平衡する時にはＲ３には電流が流れない。よって、抵抗Ｒ３は考慮しない。
※これも本番では間違えました（Ｒ３を入れちゃった）。考慮しない理由は（１）の時と同じく、解答見てから自分なりに考えた事なので、自信はほどほど、です。

（４）
後は式変形。手書き２枚目参照。

（５）
Ｗに目盛りを振る→ＲＢを指示値とする、という事。よって、ＲＱ、ＲＫを固定値→ＲＱ／ＲＫを定数とし、ＲＢの読みでＲ１を求める事ができる。

以上。

07年種理論問５、の補足。

ここの補足、です。
問題分解答内容については、ここ参照で。


静電気（静電界）の問題。普通にやれば問題なしの問題ですね。

各解答（１）～（５）については以下です。
図を見ればわかるけど、正六角形では
１辺の長さ＝頂点から中心（重心：対角線の交点）の長さ＝ｒ
です。

（１）Ｐ１－Ｐ４の距離は、図より２ｒなので、

Ｆ４＝Ｑ＾２／｛４πε０（２ｒ）＾２｝＝Ｑ＾２／（４πε０ｒ＾２）・（１／４）

となる。また、電荷は正・負であるため吸引力のため、Ｐ１では左向き。

（２）Ｐ１に対し、Ｐ２，Ｐ６は距離ｒなので、力の大きさＦ２、Ｆ６は等しく、共に負電荷であるため吸引力となる。その大きさは、

Ｆ２＝Ｆ６＝Ｑ＾２／（４πε０ｒ＾２）

となる。
この合力を考えると、Ｆ２，Ｆ６のｙ軸成分は大きさが等しく、向きが逆の為、打消しあう。
また、ｘ軸成分は、大きさ、向き共に等しくなり（左向き）、大きさは（ｒ／２）／ｒ＝１／２。よって、Ｆ２とＦ６の合力、Ｆ２６は、

Ｆ２６＝Ｑ＾２／（４πε０ｒ＾２）×（１／２）×２
　　　＝Ｑ＾２／（４πε０ｒ＾２）

となる。

（３）これも（２）と基本的には同様の考え方であるが、
・電荷は全て正のため反発力→ｙ成分は打消し合い、ｘ成分は右向き
・距離はｘ＝３ｒ／２、ｙ＝√３ｒ／２ の直角三角形の斜辺であり、√３ｒとなる。
・よって、ｘ軸成分は（３ｒ／２）／（√３ｒ）＝√３／２
これらより、

Ｆ３＝Ｆ５＝Ｑ＾２／｛４πε０（√３ｒ）＾２｝
　　＝Ｑ＾２／（４πε０ｒ＾２）・（１／３）

合力Ｆ３５は、

Ｆ３５＝Ｑ＾２／（４πε０ｒ＾２）・（１／√３）

となる。

（４）右向きを正とすると、合力Ｆは

Ｆ＝Ｆ４＋Ｆ２６＋Ｆ３５
　＝Ｑ＾２／（４πε０ｒ＾２）（１／√３－１－１／４）
　＝（４√３－１５）／１２

（５）原点における電界のうち、各電荷によるものをそれぞれＥ１～Ｅ６とする。大きさは全て等しく、Ｑ／（４πε０ｒ＾２）。ｘ軸上で向かい合う、Ｅ１とＥ４に注目すると、共に向きは左向きとなり
、合力は単純に和算でよい（電界の定義は任意の点に電荷＋１［Ｃ］を置いた時に働く力なので、正電荷では反発力、負電荷では吸引力方向の電界）。
他にも向かい合う、Ｅ２，Ｅ５及びＥ３，Ｅ６は向きが等しい。
ここで、Ｅ１，Ｅ４の合力Ｅ１４，Ｅ２，Ｅ５の合力Ｅ２５、Ｅ３，Ｅ６の合力Ｅ３６を考えると、これらは大きさが等しく、互いに１２０度ずつのベクトル。よって、全ての合力は０となる。

０７年理論試験問題補足。

ここの補足、です。

問４
（１）
電圧で式を立てており、ここにはコンデンサ電圧が入る。コンデンサでは、
ｑ＝ＣＶ、ｉ＝ｄｑ／ｄｔ→ｑ＝∫ｉｄｔ
の関係があり、これより、ｖｃ＝（１／Ｃ）∫ｉｄｔ となる。

（２）（３）
微分方程式Ｒ１ｉ＋（１／Ｃ）∫ｉｄｔ＋Ｒ２ｉ＝Ｅを解く。ここで、回路解析上、Ｒ１とＲ２は直列接続であるため、Ｚ＝Ｒ１＋Ｒ２として解く。微分方程式の両辺をラプラス変換すると、
Ｅ／Ｓ＝ＺＩ＋Ｉ／ＳＣ＋ｑｃ（０）／ＳＣ。ここで、ｑｃ（０）／Ｃは、初期条件よりＶ０であるため（ｑｃ（０）＝ｃＶ０より）、
Ｉ＝（Ｅ－Ｖ０）／｛Ｓ＋（１／ＣＺ）｝
両辺を逆ラプラス変換すると（Ｚを元に戻す）、
ｉ＝（Ｅ－Ｖ０）／（Ｒ１＋Ｒ２）ｅ^-t/C(R1+R2)
よって、ｖ＝Ｒ２ｉ＝（Ｅ－Ｖ０）・Ｒ２／（Ｒ１＋Ｒ２）ｅ^-t/C(R1+R2) となる。

（４）
ｔ→∞で、ｅ^-t/C(R1+R2)＝ｅ^-∞＝１／∞＝０。よって、ｖは初期値
（Ｅ－Ｖ０）Ｒ２／（Ｒ１＋Ｒ２）
で、時刻とともに０に漸近する。

（５）
問４より、
ｖｃ＝Ｅ－（Ｒ１＋Ｒ２）ｉ＝Ｅ－（Ｅ－Ｖ０）ｅ^-t/C(R1+R2)
であり、ｔ＝０で、ｖｃ（０）＝Ｖ０
また、ｔ＝∞で、ｖｃ（∞）＝Ｅ
よって、初期値Ｖ０で、Ｅに漸近する曲線がｖｃの電圧を表す。

※十分時間経過→Ｃのインピーダンスは∞（直流に対し１／ωＣ＝∞；コンデンサの構造を考えれば明白）→回路には電流が流れず、電圧のみが発生する。（最終的にｖｃがＥに漸近するのは、Ｒ１とＲ２と∞の直列回路→電圧は全て∞：コンデンサにかかると考えればＯＫ）また、時刻０において、Ｃのインピーダンスは０→回路はＲ１，Ｒ２の直列であり、電流ｉ（０）＝（Ｅ－Ｖ０）／（Ｒ１＋Ｒ２）となる事は、こちらも明白。このあたりの関係を使えば（４）（５）あたり、または初期値を表す（２）あたりもわかると思います（微分方程式を解ける必要はあまりない）。また、結局はＲＣ直列回路であるため、時定数がＲＣとなる一般解を知っていれば、微分方程式を全く解くことなく導出が可能です。

07年種理論問３、の補足。

ここの補足、です。

あ、さらに同時受験した３種も自己採点。３種は機械、法規が残ってたんですが…、機械は５５／１００で、１問足りない。が、例年合格点調整が行われる事が多い模様…。皆様のできが悪い事をお祈りです。法規は大丈夫と思われます。

さて、ポイントを。

問３
ポイントは下記。
（１）
重ねの理より、単純にｉ（ｔ）＝ｉ１（ｔ）＋ｉ２（ｔ）として解けば問題なしです。いや、解く必要すらないのか。多分、ｉ１がｃｏｓで与えられ、ｉ２がｓｉｎで与えられることによる引っ掛けかとは思われますが、本問はひずみ波の解析をする事、もっと言ったら電力を求める事が目的ではないので、単純に足された物を選択すればＯＫです。

（２）（３）
電源がＥ１のみのとき、角周波数ω１なので回路のインピーダンスをＺ１とすると、

Ｚ１＝Ｒ＋ｊω１Ｌ
|Ｚ１|＝√（Ｒ＾２＋（ω１Ｌ）＾２）＝√（１＾２＋４＾２）＝√１７

よって、電流波形の波高を表す、Ａ１は、

Ａ１＝Ｅ１／|Ｚ１|＝１０／√１７

また、φ１は位相角を表し、ｔａｎ^-1（虚部／実部）で表されるので、

φ１＝ｔａｎ^-1（－√１７）

ここで、“－”となっているのは、コイルは位相遅れの要素であるからである。
（電流はＥ／ｊωＬ＝－ｊＥ／ωＬと表す事ができるから）

（４）（５）
Ａ１、φ１と同様の考え方で、

|Ｚ２|＝√（１＾２＋６＾２）＝√３７。

Ａ２＝Ｅ２／|Ｚ２|＝５／√３７

φ１＝ｔａｎ^-1（－√３７）
これも、ｃｏｓ表現ｓｉｎ表現に惑う必要はなく、位相角はあくまで「電圧と電流の角度」であり、電圧と電流が同じ表現（ｃｏｓ、ｓｉｎ）をされている限りは単純に位相角を求めれば良い。ただし、仮に電圧がｃｏｓ、電流がｓｉｎなど、違う表現をされている時は、さらにπ／２ずらして変換する必要がある。そのあたりは解答群から判断する必要があり。

ここで注意点が一つ。
試験には関数電卓は持ち込み不可。なので、実質この問題は解けるの？と思い。実際、試験では勘で適当に書きました。それで今回冷静に考えてみたのですが…。

別解（もっと正しい）があるかは不明ですが、とりあえず解答の特定が可能である事はわかりました。でも、こんなの気づかないよ、試験中には…。
「関数電卓、ないじゃん！無理無理！！時間ないし！！！」ってなっちゃいますよ。

さて、その方法。条件を挙げると…、

１．上記の通り、コイルであるので、角度は負になります。よって、解答候補は４つに絞られます。（解答群については全部あげるの面倒なので）負である４つだけ挙げると、－１．３３、－１．４１、－０．１６５、－０．２４５。

２．これは知ってなきゃどうしようもない特性ですが、ｔａｎ関数は、Ｘ＞Ｙならばｔａｎ^-1Ｘ＞ｔａｎ^-1Ｙとなります。知ってなきゃ、というか、直角三角形をいくつか書いてみて、ｔａｎを考えて、角度との関係を考えればわかるのですが。これを本問に当てはめると√３７＞√１７より、|φ２|＞|φ１|となります。ここで、絶対値としたのは、本問ではφは負の値となるから。

３．最後に、角度４５度の点について考えます。この時、実部と虚部の長さが同じ（ｔａｎが１）であり、これより実部が長いか虚部が長いか、はわかれば角度が４５度以上か以下か判断できる。本問では角度は４５度以上（負側）であり、４５度をラジアン表記に変換すると、４５×（π／１８０）≒０．７８５。よって、求める|φ１|、|φ２|は共に０．７８５より大きい事になります。

１～３より、φ１、φ２は－１．３３か－１．４１であり、|φ２|＞|φ１|より、φ１＝－１．３３、φ２＝－１．４１と特定できる。

長くなりましたが、以上です。

07年種理論問２、の補足。

ここの補足、です。

自己採点の結果、理論は比較的いい点。
７～８割はいけたと思われます。
ちなみに、法規も行けたっぽい。
なんで、２種１次は無事合格、が、濃厚です…。

問２
ポイントは下記。
（１）（２）
抵抗Ｒと電圧Ｅの直流電圧源との直列接続を、電流源Ｉｘと抵抗Ｒｘの並列へと変換する問題。
結局、直列部分を取外したと考え、その端子で見た電圧（抵抗の両端電圧）が等しくなればよい。
つまり、Ｉｘ＝Ｅ／Ｒであり、Ｒｘ＝Ｒでよいことになる。
（さらに逆変換を考えると、Ｉｘ×Ｒｘが電圧源電圧と考えられるので、計算は合致する）

（３）
端子１－１’を短絡すると、並列抵抗６Ωは無視できる（分流の電流は全て抵抗なしの枝に流れる）ので、短絡した端子に流れる電流は２Ωと４Ωの抵抗による、電流源電流の分流。
さて、ここで電流源について考えると、手書きにあるように、結局は２Ａと１Ａの電流源が並列→３Ａの電流源が一個ある、と考えられ、これが分流される。

（４）
端子１－１’から見た回路網インピーダンスの逆数を考えればよい。回路網のインピーダンスは、６Ω〃（２Ω＋４Ω）と考えられ、合成インピーダンスは３Ω。
（ここで、「〃」は並列、「＋」は直列とする）

（５）
ノートンの定理は、テブナンの電流版、のような感じであり、短絡電流と回路網コンダクタンス、負荷コンダクタンスから端子開放電圧を求める定理である。
短絡電流をＩ０、回路網コンダクタンスをＹ０、負荷コンダクタンスをＹ、負荷両端電圧をＶとすると、

Ｖ＝Ｉ０／（Ｙ＋Ｙ０）

で求められる。（Ｙ＝１／Ｚです）


ちなみに…。
これをテブナンて考える（元もとの回路で）。
回路網インピーダンスは３Ω。開放端子電圧は６Ｖ（電圧源では２，４，６Ωの分圧による、６Ωの両端電圧、電流源では２Ａの電流が４Ω〃（２Ω＋６Ω）に分流され、の電流による、６Ωでの電圧降下分、これら二つの電圧を足すと６Ｖになる）。
なので、負荷に３Ωを接続すると、テブナンの定理より、負荷電流Ｉは、

Ｉ＝Ｖ／（Ｚ＋Ｚ０）＝６／（３＋３）＝１

であり、負荷は３Ωであるため負荷での電圧降下は３×１＝３Ｖとなる。

開放端子電圧を求めるのに、電流源変換後で考えるなら３Ａの電流源の分流、で、６Ωの電圧降下を考えても同じ。

さらに、閉路解析法（キルヒホッフとか）でも電圧・電流自体は解けるはず（さすがにここまではやってないですが）だし、今回細かい計算に重ねの理を使ってますが、それだけで一気に解く事も可能。

重要なのは「解けること」ですので、どんな方法でも解ければいいのだと思っています。本来は。ただ、電験においては、特に２種ではこのように、解き方を指定される事があります。微分方程式を、ラプラス変換で解きたいのに一般解から解かされたり。

なので、得意の方法を一つずつ身につけ、最悪でも求めたい回路は解析できるようにする必要はあると思います。その上で、知らない定理でも逆算で解く事は可能なはず…。

と言う感じで、この問は以上です。

２種理論 ０７年の問題 問１の補足

補足

ここの補足、です。

いよいよ終わった07年一次試験。しばらくは、解答編ですね。
（一日１〜２問の、スローペースにて）

問１
ポイントは下記。

（１）断面積Ｓ、長さｌの磁気抵抗Ｒは、透磁率をμとすると、

Ｒ１＝ｌ／μＳ

また、空げき部（幅ｄ）では、透磁率はμ０なので、

Ｒ０＝ｄ／μ０Ｓ

（Ｒ＝Ｒ１＋Ｒ０）
となる。

（２）
巻線１、２それぞれの自己インダクタンスをＬ１、Ｌ２とすると、

Ｌ１＝Ｎ１＾２／Ｒ、Ｌ２＝Ｎ２＾２／Ｒ

また、相互インダクタンスＭは、片方の巻線に電流を流して発生した磁束にて他方の磁束に誘起される磁束の割合にて定義されるため、巻線１に電流Ｉを流したとすると、

Φ１＝Ｌ１Ｉ／Ｎ１＝Ｎ１Ｉ／Ｒ

よって、Ｍ＝Ｎ２Φ１／Ｉ＝Ｎ１Ｎ２／Ｒ

ここから、Ｌ１に対する倍率が求められる。

（３）（４）（５）

巻線２に誘起される電圧は、電流の時間微分に相互インダクタンスを掛けたものとなる。と、いうか、インダクタンスは、電流時間変化分（微分）と電圧の比を表すものであり、この場合は巻線２自身で流れる電流はない（→ｉ２は０：しかも、端子開放だし）ので、巻線２の自己インダクタンスＬ２は考慮しなくてよい。

よって、相互インダクタンスと、電流ｉ１の微分を掛ければｖ２が求められる。

さて、ここで微分の式を変形する事を考えてみる。

ｄｉ１／ｄｔを変形し、左辺にｄｉ１、右辺にｄｔがくるようにし、両辺の積分を考える。積分範囲として、時間ｔ：０→∞を考えると、ｔ＝∞に対応する電流ｉ１は、

ｉ１（ｔ＝∞）＝Ｅ／ｒとなる。

これは、電源は直流であり、直流に対して定常状態（時刻∞）でのコイルのインピーダンスは０となるからである（つまり、抵抗はＲのみで、電流はＥ／ｒ）。

さらに、この積分を解いて（定数の積分なので、解くというほどでもないけど…）、相互インダクタンスの関数が求められる。

以上。